Lift Model
The Inforum approach to modeling attempts to provide both the dynamics and high-level accounting of macroeconomic models and the industry structure featured in the general equilibrium approach to modeling. The Long-term Interindustry Forecasting Tool (LIFT) is a dynamic general equilibrium representation of the U.S. national economy. It combines an interindustry input-output (I-O) formulation with extensive use of regression analysis to employ a "bottom-up" approach to macroeconomic modeling. In this way, the model works like the actual economy, building the macroeconomic totals from details of industry activity, rather than by distributing predetermined macroeconomic quantities among industries. For example, aggregate investment, total exports, and employment are not determined directly, but are computed as the sum of their parts: investment by industry, exports by commodity, and employment by industry. LIFT contains full demand and supply accounting for 110 productive sectors.
This bottom-up technique provides several desirable properties for analyzing the economy. First, the model describes how changes in one industry, such as increasing productivity or changing international trade patterns, affect related sectors and the aggregate quantities. Second, parameters in the behavioral equations differ among products, reflecting differences in, for instance, consumer preferences, price elasticities in foreign trade, and industrial structure. Third, the detailed level of disaggregation permits the modeling of prices by industry, allowing one to explore the causes and effects of relative price changes.
Another important feature of the model is the dynamic determination of endogenous variables. LIFT is an annual model, solving year by year, and it incorporates key dynamics that include investment and capital stock formation. For example, investment depends on a distributed lag in the growth of investing industries and international trade depends on a distributed lag of foreign price changes. Moreover, parameter estimates for structural equations largely are based on time-series regressions, thereby reflecting the dynamic behavior of the economic data underlying the model. Therefore, model solutions are not static, but instead they project a time path for the endogenous quantities. The LIFT model thus simulates the economy year-by-year, allowing analysts to examine both the ultimate economic impacts of projected energy or environmental policies and the dynamics of the economy's adjustment process over time.
Despite its industry basis, LIFT is a general equilibrium model, using bottom-up accounting to determine macroeconomic quantities that are consistent with the underlying industry detail. It includes macroeconomic variables that are consistent with the National Income and Product Accounts (NIPA) and other published data. This macroeconomic "superstructure" contains key functions for household savings behavior, interest rates, exchange rates, unemployment, taxes, government spending, and current account balances. Like many aggregate macroeconomic models, this structure is configured to make LIFT exhibit "Keynesian" demand-driven behavior over the short run but neoclassical growth characteristics over the longer term. For example, while monetary and fiscal policies and changes in exchange rates can affect the level of output in the short-to-intermediate term, supply forces - available labor, capital, and technology - will determine the level of output in the long term.
The LIFT model thus is particularly suited for examining and assessing the macroeconomic and industry impacts of the changing composition of consumption, production, foreign trade, and employment as the economy grows through time.
The interindustry framework underlying the model is composed of five blocks: final demand, supply, factor income, prices, and the accountant. The first block of LIFT uses econometric equations to predict the behavior of real final demand (consumption, investment, imports, exports, and government expenditures). The components are modeled at various levels of detail. For example, aggregate consumption is the sum of 83 consumption products, and aggregate construction investment is the sum of expenditures for 19 types of private structures. Demand by product, with product sectors consistent with the input-output table (A matrix), is determined using bridge matrices to convert final demand to the commodity level. Following Wilson (2001), this equation is specified as:
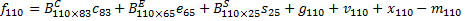
where B represents a bridge matrix for the various components (consumption, equipment investment by purchasing industry, and construction by type ) and where remaining variables represent consumption by product, equipment investment by purchasing industry, structures by type, inventory change, exports and imports, and government spending.
In the supply block, these detailed demand predictions then are used in an input-output production identity to calculate real gross output:
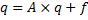
where q and f are vectors of output and final demand by commodity, respectively, each having 110 elements, and where A is a 110x110 matrix of input-output coefficients. Input-output coefficients and the bridge matrix coefficients vary over time according to historical trends evident in available data and, in some cases, using assumptions about how technology and tastes might develop in the future (Almon 2008).
Commodity prices are determined in a similar fashion. In the factor income block, econometric behavioral equations predict each value-added component (including compensation, profits, interest, rent, and indirect taxes) by industry. Labor compensation depends on industry-specific wages that are determined by industry-specific factors as well as overall labor market conditions. Profit margins are dependent on measures of industry slack (excess supply or demand) and, for tradable sectors, on international prices. Depreciation depends on capital stock levels. Indirect taxes and subsidies are imposed, in most cases, through exogenous ad-valorum rates on overall nominal output.
The industry value added levels are allocated to production commodities using a make matrix. Then the fundamental input-output price identity combines value added per unit of output with unit costs of intermediate goods and services to form an indicator of commodity prices:
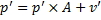
where p and v have 110 elements to represent production prices and unit value added, respectively. This identity ensures that income, prices, and output by sector are directly related and are consistent. In turn, relative prices and income flows are included as independent variables in the regression equations for final demand, creating simultaneity between final demand and value added.
As noted above, LIFT also calculates all of the major nominal economic balances for an economy: personal income and expenditure, the government fiscal balance (at both the federal and state and local government levels), and the current account balance. It also contains a full accounting for population, the labor force, and employment. This content is important for building alternative simulations because it ensures consistency between economic growth determined on the product side and the inflation and income components. The model allows us to examine how alternative microeconomic conditions or policies will affect other aspects of the economy. Because the input-output structure allows a bottom-up approach to modeling the macro economy, macroeconomic results fully are consistent with simulated industry disruptions.
Recent projects include analyses of the effects of the sequester and other recent changes to fiscal policy (Werling 2012) and analysis of the harm done by policies that allow deterioration of infrastructure (Werling 2012). Long-run economic effects of technological development were assessed in Meade (2010), in the case of vehicle electrification, and in Meade (2009) for the case of policies that encourage technological development to combat climate change. Examples of impact analysis conducted with the Lift model include a study of the economic effects of port closures following a terroristic attack (reported in CBO, 2006, and in two private studies) and the economic impacts of the September 2001 attacks (Werling and Horst, 2009). Other studies of macro and industry impacts of supply constraints include the "Macroeconomic and Industrial Effects of Higher Natural Gas Prices" and "Immigration Impacts on the U.S. Economy," delivered to the Department of Commerce in 2006.
